Diện tích tứ giác và các công thức tính toán cơ bản

Diện tích tứ giác là một trong những kiến thức cơ bản mà học sinh cần nắm vững khi học môn hình học. Tuy nhiên, sự đa dạng của các loại tứ giác khiến cho việc tính toán diện tích trở nên thú vị và đôi khi cũng khá phức tạp. Trong bài viết này, Cmath sẽ hướng dẫn các em cách tính diện tích tứ giác một cách chi tiết, dễ hiểu và hiệu quả nhất.

Khái Niệm Cơ Bản Về Hình Tứ Giác

Tứ Giác Là Gì?

Tứ giác là một đa giác có 4 cạnh và 4 đỉnh, và không có bất kỳ hai đoạn thẳng nào cùng nằm trên một đường thẳng. Nói cách khác, hình tứ giác được bao quanh bởi 4 đoạn thẳng nối liền nhau, tạo thành một hình phẳng.

Các Loại Tứ Giác Cơ Bản

Có một số loại tứ giác mà học sinh cần biết, bao gồm:

• Tứ giác đơn: Là tứ giác không có cạnh nào cắt nhau.
• Tứ giác lồi: Là tứ giác đơn mà tất cả các góc trong đều nhỏ hơn 180 độ.
• Tứ giác lõm: Là tứ giác đơn có ít nhất một góc lớn hơn 180 độ.
• Tứ giác nội tiếp: Là tứ giác có cả 4 đỉnh cùng nằm trên một đường tròn.
• Tứ giác ngoại tiếp: Là tứ giác có cả 4 cạnh đều tiếp xúc với một đường tròn.

Các loại tứ giác đặc biệt thường được sử dụng trong Toán học như hình bình hành, hình chữ nhật, hình thoi, và hình vuông. Những hình tứ giác này không chỉ xuất hiện trong sách giáo khoa mà còn trong nhiều lĩnh vực khác nhau như kiến trúc, xây dựng, và thiết kế đồ họa.

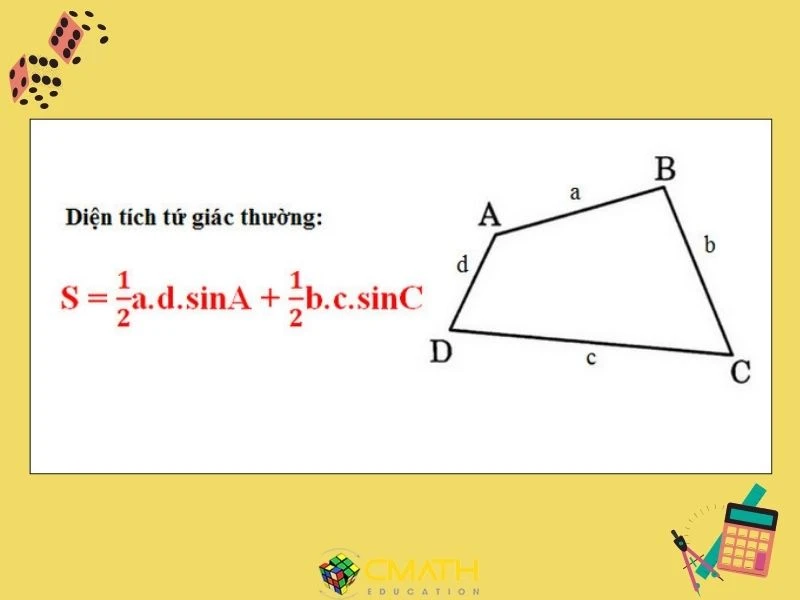
Công Thức Tính Diện Tích Hình Tứ Giác Là Gì?

Tứ giác là một hình học cơ bản, nhưng sự đa dạng của các loại tứ giác khiến việc tính toán diện tích trở nên phức tạp. Không có một công thức chung nào áp dụng cho tất cả các loại tứ giác, và mỗi loại tứ giác lại có những đặc điểm riêng biệt.

Các Công Thức Cụ Thể Để Tính Diện Tích

Dưới đây là tổng hợp công thức tính diện tích cho một số loại tứ giác đặc biệt:

Cách Tính Diện Tích Hình Vuông

Hình vuông có bốn cạnh bằng nhau. Để tính diện tích, ta chỉ cần nhân độ dài một cạnh với chính nó.

• Công thức tính diện tích hình vuông:

S = a x a Trong đó: - S: Diện tích hình vuông. - a: Độ dài một cạnh của hình vuông.

Công Thức Tính Diện Tích Hình Chữ Nhật

Hình chữ nhật có chiều dài và chiều rộng khác nhau. Để tính diện tích, ta nhân chiều dài với chiều rộng.

• Công thức tính diện tích hình chữ nhật:

S = a x b Trong đó: - S: Diện tích hình chữ nhật. - a: Chiều dài của hình chữ nhật. - b: Chiều rộng của hình chữ nhật.

Công Thức Tính Diện Tích Hình Bình Hành

Hình bình hành là một tứ giác có hai cặp cạnh đối diện song song và bằng nhau.

• Công thức tính diện tích hình bình hành:

S = a x h Trong đó: - S: Diện tích hình bình hành. - a: Độ dài đáy của hình bình hành. - h: Chiều cao tương ứng với đáy đã chọn.

Cách Tính Diện Tích Hình Thoi

Hình thoi có hai đường chéo vuông góc với nhau. Diện tích hình thoi bằng một nửa tích của hai đường chéo.

• Công thức tính diện tích hình thoi:

S = (d1 x d2) / 2 Trong đó: - S: Diện tích hình thoi. - d1, d2: Độ dài hai đường chéo của hình thoi.

Công Thức Tính Diện Tích Hình Thang

Hình thang có hai cạnh đáy song song nhưng không bằng nhau. Để tính diện tích hình thang, ta có thể sử dụng công thức sau.

• Công thức tính diện tích hình thang:

S = ½ (a + b) x h Trong đó: - S: Diện tích của hình thang. - a, b: Độ dài hai đáy của hình thang. - h: Chiều cao của hình thang.

Một Vài Dạng Toán Tính Diện Tích Hình Tứ Giác Thường Gặp

Trong thực tế, có rất nhiều bài tập liên quan đến cách tính diện tích hình tứ giác. Dưới đây là hai dạng toán thường gặp mà học sinh cần chú ý:

Dạng 1: Tính Diện Tích Khi Biết Một Cạnh Và Đường Cao

Bài toán này thường yêu cầu tính diện tích của các tứ giác đặc biệt như hình vuông, hình chữ nhật hay hình thang. Học sinh chỉ cần áp dụng công thức để có được kết quả chính xác.

Dạng 2: Cho Diện Tích, Tính Cạnh Và Đường Cao

Đây là bài toán ngược của dạng 1. Để giải bài tập này, học sinh cần áp dụng công thức tính diện tích rồi suy luận ra công thức tính cạnh hoặc chiều cao tương ứng.

Bài Tập Về Công Thức Tính Diện Tích Hình Tứ Giác Tự Ôn Luyện Tại Nhà

Dưới đây là một số bài tập mà các em có thể tự ôn luyện tại nhà:

• Bài tập 1: Cho hình vuông ABCD có cạnh AB = 5cm. Tính diện tích hình vuông ABCD.
• Bài tập 2: Một hình chữ nhật có chiều dài 8cm, chiều rộng bằng 3/4 chiều dài. Tính diện tích hình chữ nhật đó.
• Bài tập 3: Hình bình hành MNPQ có độ dài đáy MN = 12cm, chiều cao KH = 8cm. Tính diện tích hình bình hành MNPQ.
• Bài tập 4: Một hình thang cân có độ dài hai đáy lần lượt là 6cm và 10cm, chiều cao bằng 5cm. Tính diện tích hình thang cân đó.
• Bài tập 5: Cho hình thoi ABCD có độ dài hai đường chéo AC = 10cm, BD = 12cm. Tính diện tích hình thoi ABCD.
• Bài tập 6: Một mảnh đất hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Biết chiều rộng là 5m. Người ta trồng rau trên mảnh đất đó, cứ 1m² thu hoạch được 2kg rau. Hỏi cả mảnh đất thu hoạch được bao nhiêu ki-lô-gam rau?
• Bài tập 7: Cho hình thang vuông ABCD có góc A và góc D vuông, AB = 6cm, CD = 10cm, AD = 4cm. Tính diện tích hình thang ABCD.
• Bài tập 8: Một hình bình hành có diện tích là 48cm², chiều cao tương ứng với một cạnh đáy là 6cm. Tính độ dài cạnh đáy đó.
• Bài tập 9: Cho hình thoi ABCD có cạnh AB = 5cm, góc A = 60 độ. Tính diện tích hình thoi ABCD.
• Bài tập 10: Một mảnh đất hình thang có đáy lớn 30m, đáy bé 20m, chiều cao 12m. Người ta dành 30% diện tích đất để làm nhà. Tính diện tích phần đất còn lại.

Tư Duy Toán Học Nâng Cao, Giải Bài Tập Đơn Giản Tại Cmath

Đối với nhiều học sinh, môn Toán có thể là một thách thức lớn, đặc biệt là trong lĩnh vực hình học. Để giúp các em phát triển tư duy và kỹ năng giải quyết vấn đề, việc tìm một môi trường học tập tốt là rất quan trọng. Câu lạc bộ Toán học muôn màu Cmath chính là một lựa chọn tuyệt vời cho các bậc phụ huynh. Chương trình học tại Cmath được thiết kế bởi thầy Võ Quốc Bá Cẩn và đội ngũ giáo viên giàu kinh nghiệm. Chương trình không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề một cách sáng tạo.

Tại Sao Chọn Cmath?

• Phương pháp học tập hiện đại: Chương trình học kết hợp giữa kiến thức cơ bản và nâng cao.
• Đội ngũ giảng viên chất lượng: Các thầy cô có nhiều kinh nghiệm và nhiệt huyết trong việc dạy học.
• Môi trường học tập thân thiện: Nơi các em có thể thoải mái giao lưu và học hỏi lẫn nhau.

Trên đây là những thông tin cần thiết về công thức tính diện tích tứ giác mà các em học sinh cần nắm rõ. Nếu bạn đang tìm kiếm một môi trường học tập tốt cho con mình, hãy đến ngay với Câu lạc bộ Toán học Cmath!

Xem Thêm:

• Bật mí công thức tính diện tích hình Elip đơn giản, chính xác.
• Công thức tính diện tích hình bình hành và bài tập chi tiết.
• Công thức tính diện tích hình tròn và các bài tập thường gặp.

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về diện tích tứ giác. Hãy cùng nhau khám phá thêm nhiều điều thú vị khác trong môn Toán học nhé!