Diện tích tứ giác đều trong khối chóp tứ giác đều

Khối chóp tứ giác đều là một trong những hình khối quan trọng trong hình học không gian. Để giúp các bạn hiểu rõ hơn về khối chóp này, trong bài viết dưới đây, chúng ta sẽ đi sâu vào định nghĩa, tính chất, công thức tính thể tích và diện tích của khối chóp tứ giác đều, cùng với một số bài tập vận dụng.

1. Khối Chóp Tứ Giác Đều Là Gì?

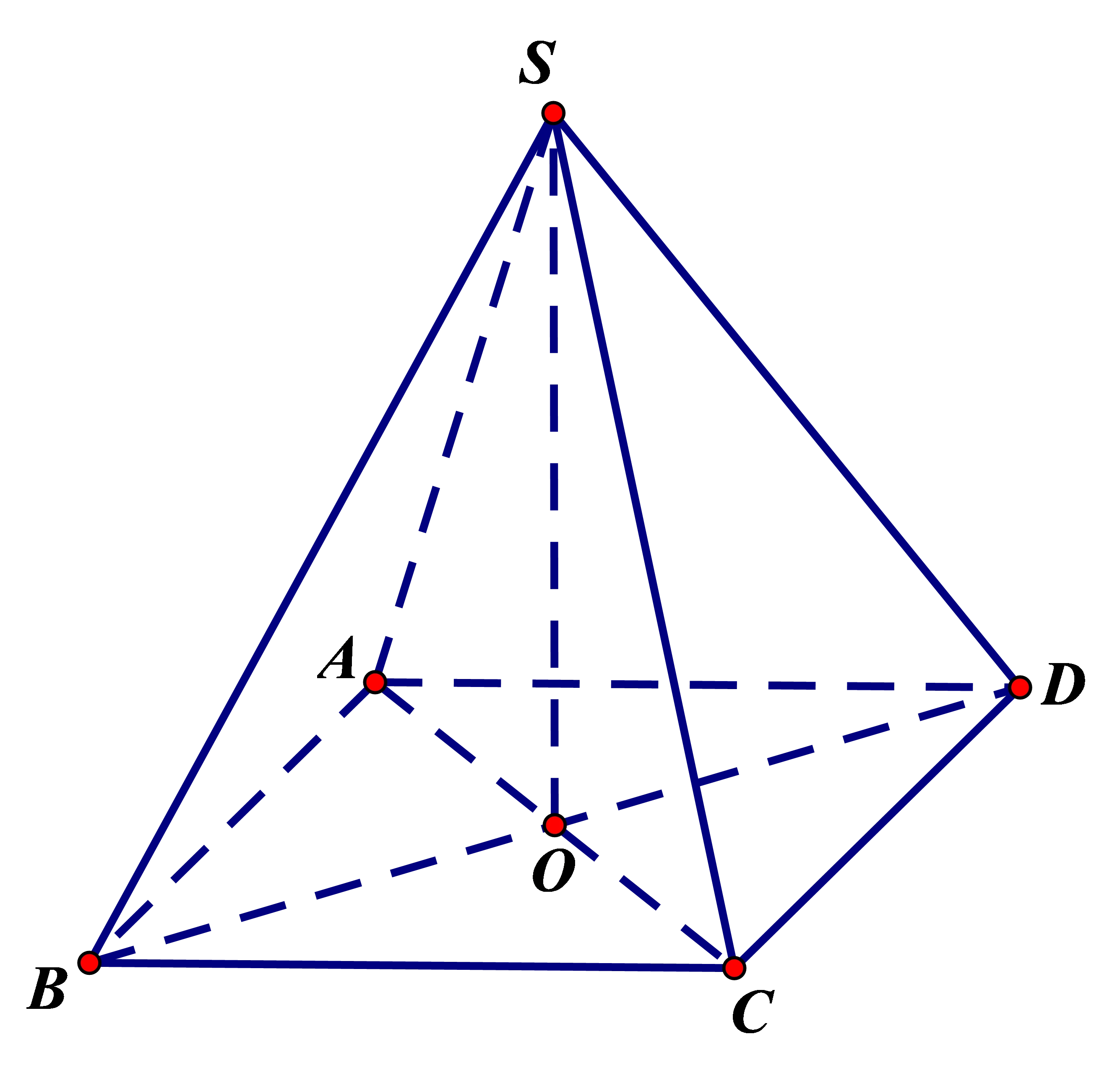
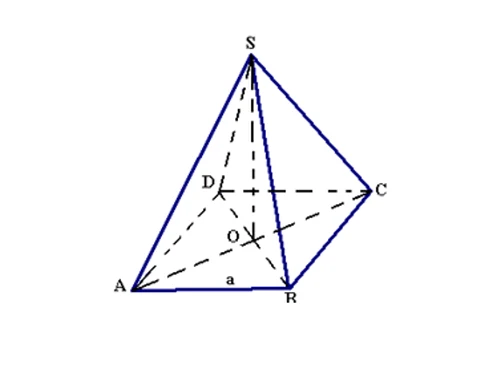
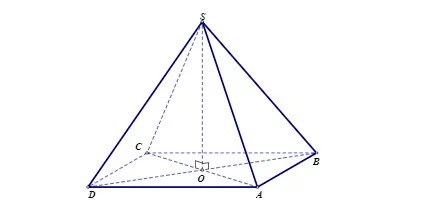
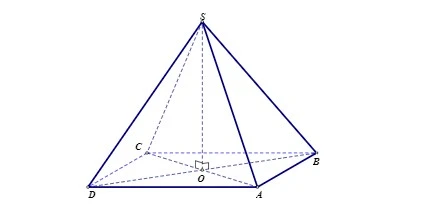
Khối chóp tứ giác đều là hình chóp có đáy là hình vuông, và đường cao của chóp đi qua tâm đáy, tức là giao của hai đường chéo của hình vuông. Hình chóp này có các cạnh bên đều nhau và các mặt bên là các tam giác cân.

2. Tính Chất Của Khối Chóp Tứ Giác Đều

Khối chóp tứ giác đều có nhiều tính chất nổi bật, bao gồm:

• Cạnh bên bằng nhau: Tất cả các cạnh bên của khối chóp tứ giác đều đều có chiều dài bằng nhau.
• Đáy là hình vuông: Đáy của khối chóp là một hình vuông, với các cạnh bằng nhau.
• Chân đường cao trùng với tâm mặt đáy: Đường cao của khối chóp đi qua tâm của hình vuông đáy.
• Các mặt bên là các tam giác cân: Các mặt bên của khối chóp đều là tam giác cân, có độ dài hai cạnh bằng nhau.
• Các góc tạo bởi cạnh bên và mặt đáy bằng nhau: Tất cả các góc tạo bởi cạnh bên và mặt đáy đều có độ lớn bằng nhau.
• Các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau: Góc giữa các mặt bên và mặt đáy cũng giống nhau.

Ví dụ:

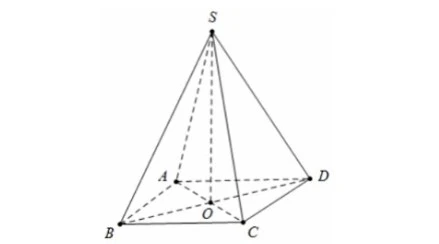
Với hình chóp tứ giác đều SABCD, ta có:

• Tứ giác ABCD là hình vuông với tâm O.
• SO ⊥ (ABCD).
• SA = SB = SC = SD.
• Các góc giữa SA và mặt đáy (ABCD) đều bằng nhau.

3. Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều

Thể tích của khối chóp tứ giác đều được tính theo công thức: \[ V = \frac{1}{3} \cdot S_{đáy} \cdot h \] Trong đó:

• V: Thể tích hình chóp tứ giác đều.
• h: Chiều cao của hình chóp tứ giác đều.
• S_{đáy}: Diện tích đáy của hình chóp tứ giác đều.

4. Công Thức Tính Diện Tích Khối Chóp Tứ Giác Đều

4.1. Tính Diện Tích Xung Quanh

Diện tích xung quanh của khối chóp tứ giác đều được tính bằng công thức: \[ S_{xq} = 4 \cdot S \] Trong đó:

• S_{xq}: Diện tích xung quanh của hình chóp tứ giác đều.
• S: Diện tích mặt bên của hình chóp tứ giác đều.

4.2. Tính Diện Tích Toàn Phần

Diện tích toàn phần của khối chóp tứ giác đều được tính như sau: \[ S_{tp} = S_{xq} + S_{đáy} \] Trong đó:

• S_{tp}: Diện tích toàn phần của hình chóp tứ giác đều.
• S_{xq}: Diện tích xung quanh của hình chóp tứ giác đều.
• S_{đáy}: Diện tích đáy của hình chóp tứ giác đều.

5. Một Số Bài Tập Tính Thể Tích Khối Chóp Tứ Giác Đều (Kèm Lời Giải Chi Tiết)

Câu 1:

Cho S.ABCD là hình chóp đều. Tính thể tích khối chóp S.ABCD biết AB = a; SA = a. Giải:

• Diện tích của đáy ABCD là \( S_{ABCD} = a^2 \).
• Chiều cao \( SH = \sqrt{SA^2 - AH^2} = \frac{a \sqrt{2}}{2} \).
• Vậy thể tích \( V_{S.ABCD} = \frac{1}{3} S_{ABCD} \cdot SH = \frac{1}{3} a^2 \cdot \frac{a\sqrt{2}}{2} = \frac{a^3\sqrt{2}}{6} \).

Câu 2:

Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a. Giải:

• Diện tích đáy ABCD là \( a^2 \).
• Chiều cao \( SO = \frac{a\sqrt{2}}{2} \).
• Thể tích \( V_{S.ABCD} = \frac{1}{3} \cdot a^2 \cdot \frac{a\sqrt{2}}{2} = \frac{a^3\sqrt{2}}{6} \).

Câu 3:

Cho hình chóp tứ giác đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích khối chóp. Giải:

• Thể tích khối chóp được tính theo công thức:

\[ V = \frac{1}{3} B \cdot h \] với \( B = x^2 \).

• Gọi chiều dài của đoạn \( SO = h \).

Lưu Ý: Các bài tập trên chỉ là ví dụ. Các bạn có thể tham khảo thêm nhiều dạng bài tập khác nhau để nắm vững kiến thức.

6. Kết Luận

Hy vọng rằng sau bài viết này, bạn đã có cái nhìn tổng quan và rõ ràng hơn về khối chóp tứ giác đều, từ định nghĩa, tính chất cho đến các công thức tính toán. Hãy luyện tập thật nhiều với các bài tập để củng cố kiến thức của mình. Để có thêm nhiều kiến thức hay về công thức toán hình, bạn có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản và chuẩn bị tốt cho kỳ thi đại học sắp tới nhé! Tham khảo thêm:

• Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết

Chúc bạn học tập hiệu quả và thành công!