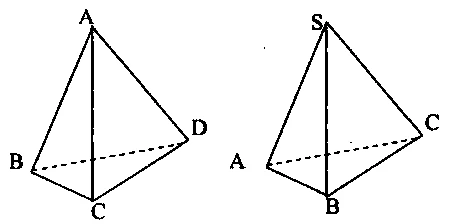
Khối tứ diện, một khối hình trong không gian được hình thành từ bốn điểm không nằm trên cùng một mặt phẳng, đã trở thành một chủ đề thú vị trong hình học không gian. Chúng ta sẽ khám phá công thức tính thể tích của khối tứ diện, cách áp dụng và một số dạng bài tập liên quan đến nó.
1. Kiến Thức Cơ Bản Về Khối Tứ Diện
1.1 Tứ Diện
Tứ diện có bốn mặt, trong đó mỗi mặt đều là hình tam giác. Một số loại tứ diện phổ biến bao gồm:
- Tứ diện đều: có tất cả các cạnh bằng nhau và các mặt là tam giác đều.
- Tứ diện không đều: có các cạnh và mặt không giống nhau.
1.2 Công Thức Tính Thể Tích
Thể tích của tứ diện có thể được tính bằng công thức sau:
\[ V = \frac{1}{3} S_{BCD} \cdot AH \]
Trong đó:
- \( V \) là thể tích của tứ diện,
- \( S_{BCD} \) là diện tích của mặt đáy,
- \( AH \) là chiều cao từ đỉnh \( A \) tới mặt đáy \( BCD \).
1.3 Diện Tích Của Tứ Diện Đều
Đối với tứ diện đều, công thức tính thể tích được đơn giản hóa hơn:
\[ V = \frac{a^3}{6\sqrt{2}} \]
Trong đó \( a \) là độ dài của cạnh.
2. Các Bài Tập Ứng Dụng
Để hiểu rõ hơn về việc áp dụng công thức tính thể tích khối tứ diện, hãy cùng xem xét một số bài toán điển hình.
Bài Toán 1: Tính Thể Tích Tứ Diện Đều
Cho tứ diện đều \( ABCD \) với cạnh \( a \). Tính thể tích \( V \) của hình này.
\[
V = \frac{a^3}{6\sqrt{2}}
\]
Bài Toán 2: Tính Thể Tích Tứ Diện Gần Đều
Cho tứ diện gần đều với các cặp cạnh đối bằng nhau: \( AB = CD = a, AC = BD = b, AD = BC = c \). Tính thể tích \( V \).
Dựng một tứ diện khác để áp dụng cách tính thể tích.
\[
V_{ABCD} = \frac{\sqrt{2}}{12} \sqrt{(-a^2 + b^2 + c^2)(a^2 - b^2 + c^2)(a^2 + b^2 - c^2)}
\]
3. Một Số Công Thức Bổ Sung
3.1 Thể Tích Tứ Diện Qua Các Đường Thẳng
Công thức tính thể tích tứ diện qua các đường thẳng cũng rất quan trọng:
\[
V = \frac{1}{6}abCD \sin \alpha
\]
Trong đó:
- \( AB \) và \( CD \) là độ dài của các cạnh,
- \( d \) là khoảng cách giữa hai đường thẳng,
- \( \alpha \) là góc giữa hai hướng.
3.2 Tính Khoảng Cách Giữa Hai Đường Chéo
Để tìm khoảng cách giữa hai đường chéo của tứ diện, ta có thể sử dụng định lý Pythagore trong tam giác vuông.
4. Các Ứng Dụng Của Thể Tích Khối Tứ Diện
4.1 Trong Kiến Trúc
Trong lĩnh vực kiến trúc, thể tích khối tứ diện được ứng dụng trong việc tính toán không gian xây dựng. Các mái nhà có hình dạng khối tứ diện thường được thiết kế để tối ưu hóa diện tích.
4.2 Trong Khoa Học Vật Liệu
Thể tích tứ diện cũng được tận dụng trong khoa học vật liệu để tính toán khối lượng và tỷ trọng của các vật thể có hình dạng gần giống như tứ diện.
4.3 Trong Thiết Kế Các Mô Hình 3D
Trong đồ họa máy tính, thể tích tứ diện đóng vai trò quan trọng trong việc mô phỏng và dựng hình các đối tượng 3D.
5. Kết Luận
Khối tứ diện không chỉ là một chủ đề lý thuyết mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực. Việc nắm vững công thức và phương pháp tính thể tích sẽ giúp ích rất nhiều trong học tập và công việc thực tế. Hy vọng rằng qua bài viết này, bạn đã có cái nhìn rõ hơn về thể tích khối tứ diện và các ứng dụng của nó. Hãy cùng thực hành nhiều bài tập để củng cố và nâng cao kỹ năng của mình!